Путенихин Петр Васильевич
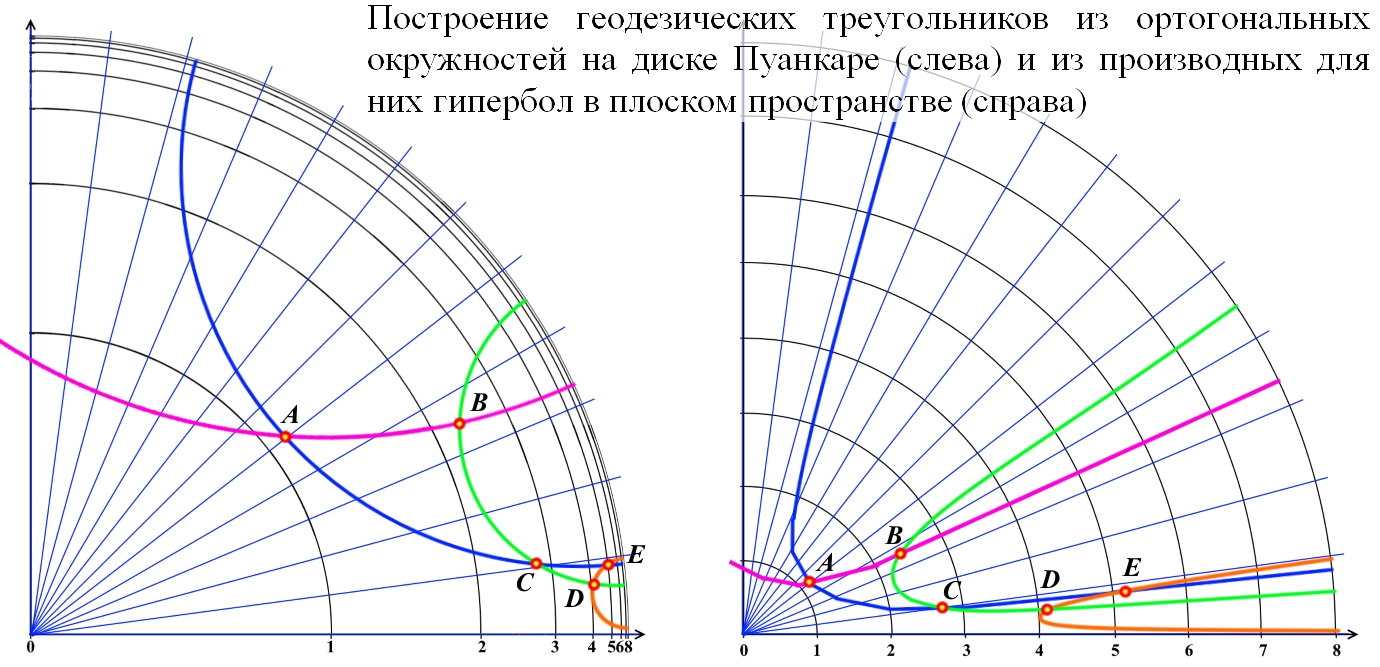
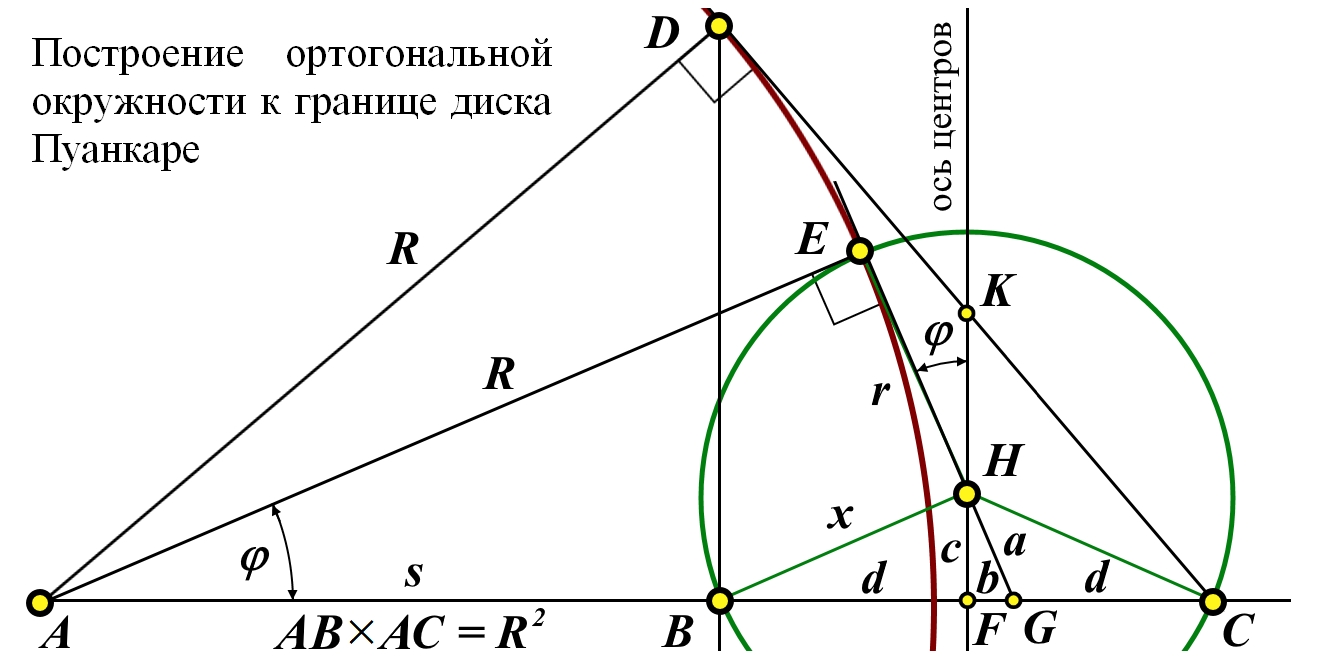
Трёхмерное пространство отрицательной кривизны. Сфера Лобачевского

Lib.ru/Современная: [Регистрация] [Найти] [Рейтинги] [Обсуждения] [Новинки] [Помощь]
  • Оставить комментарий
  • © Copyright Путенихин Петр Васильевич (pe_put@rambler.ru)
  • Размещен: 14/11/2021, изменен: 14/11/2021. 36k. Статистика.
  • Статья: Естеств.науки
  • Иллюстрации/приложения: 9 шт.
  • Скачать FB2
    •  Ваша оценка:
  • Аннотация:
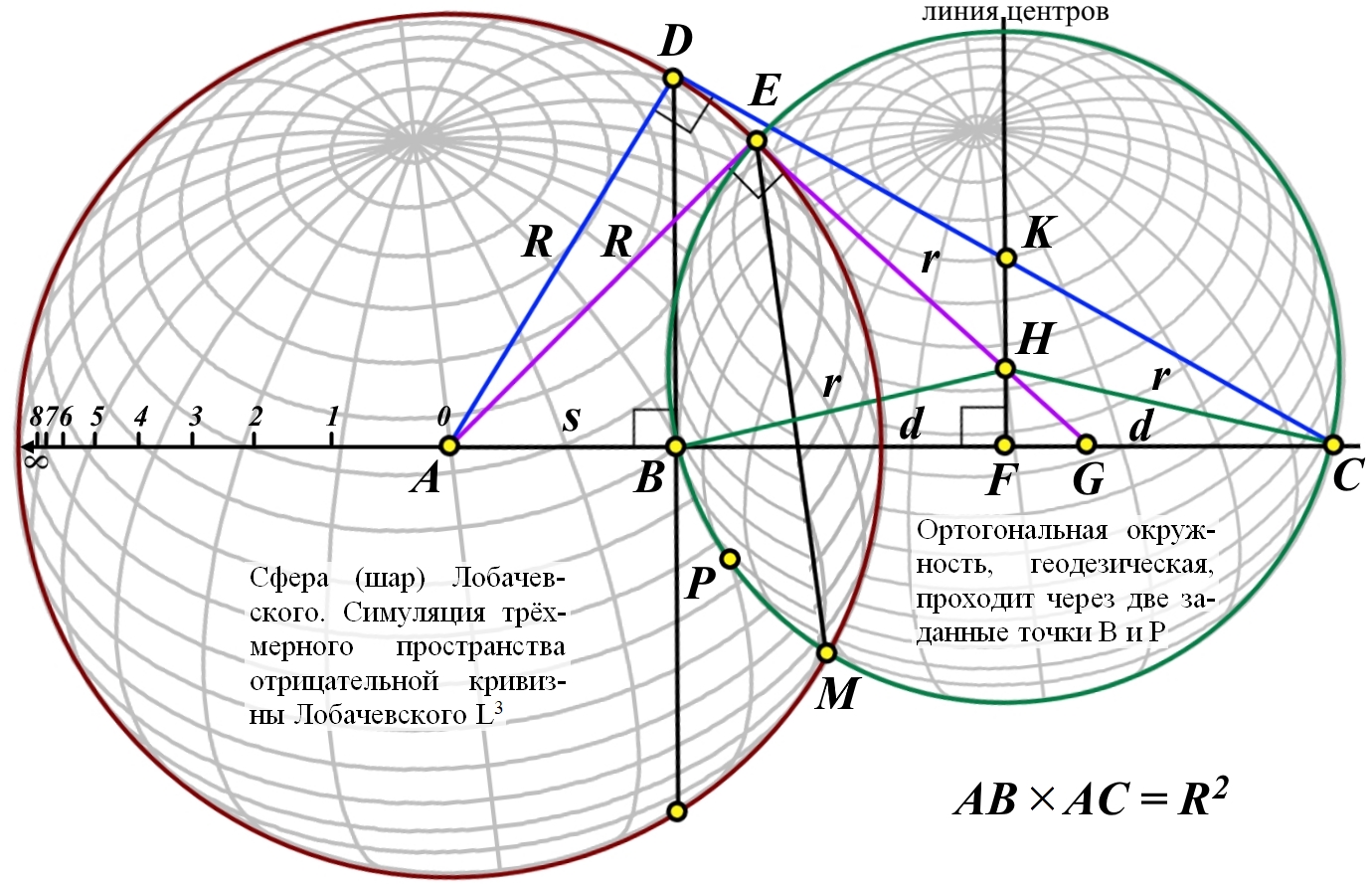
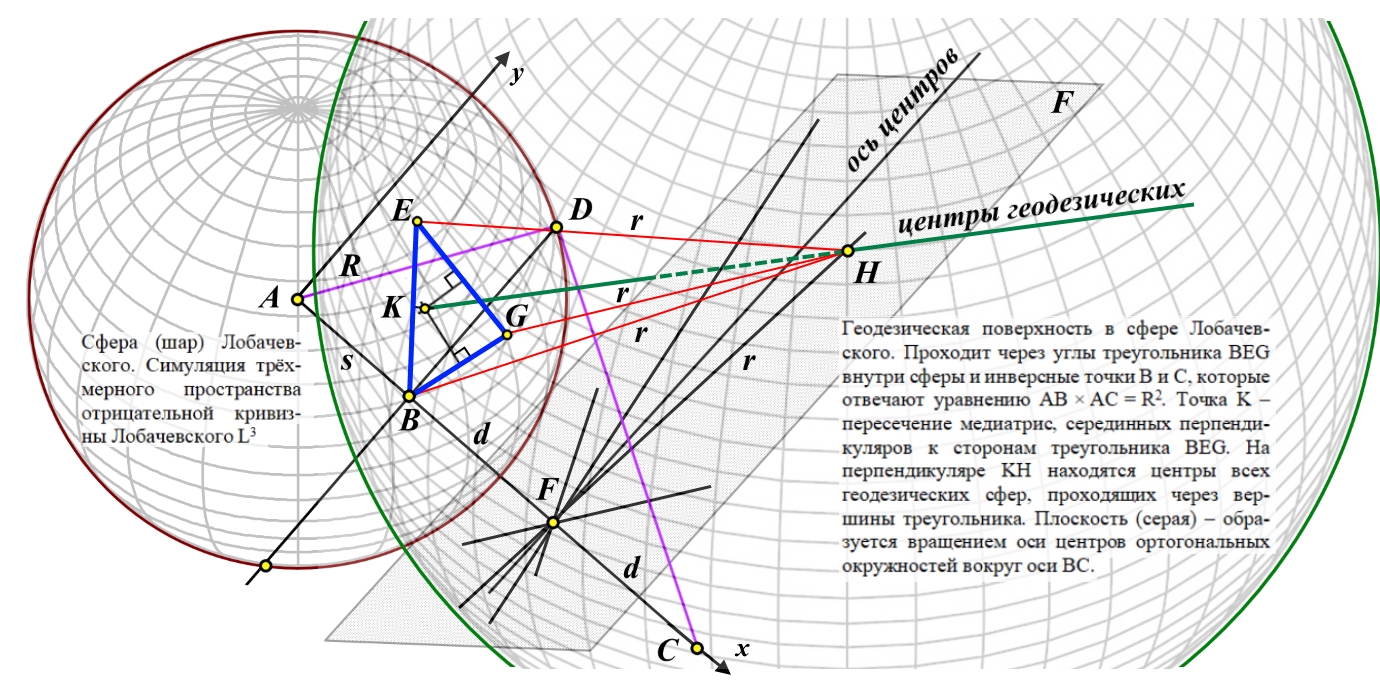
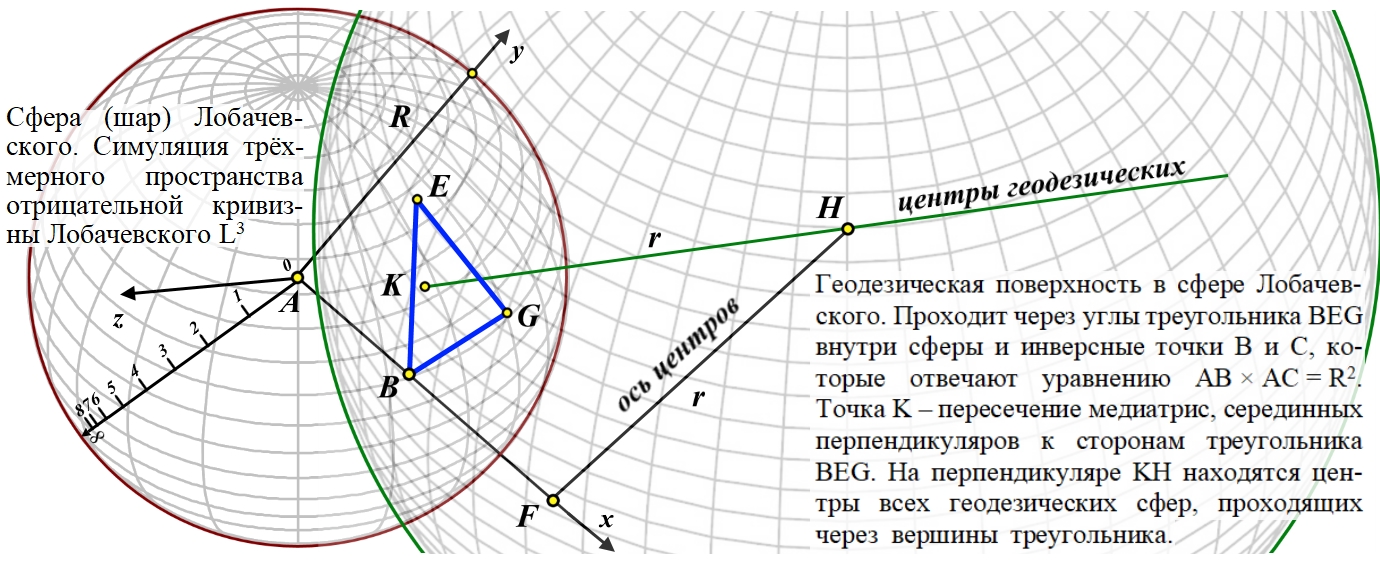
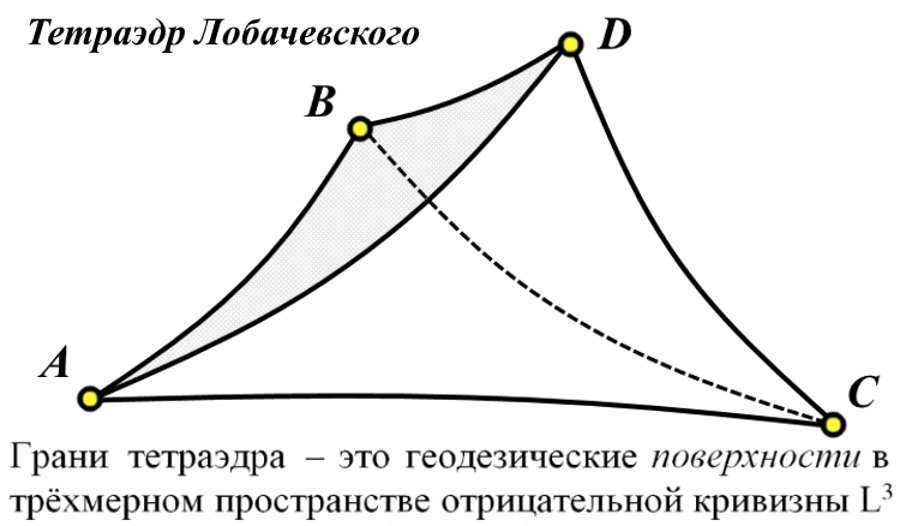
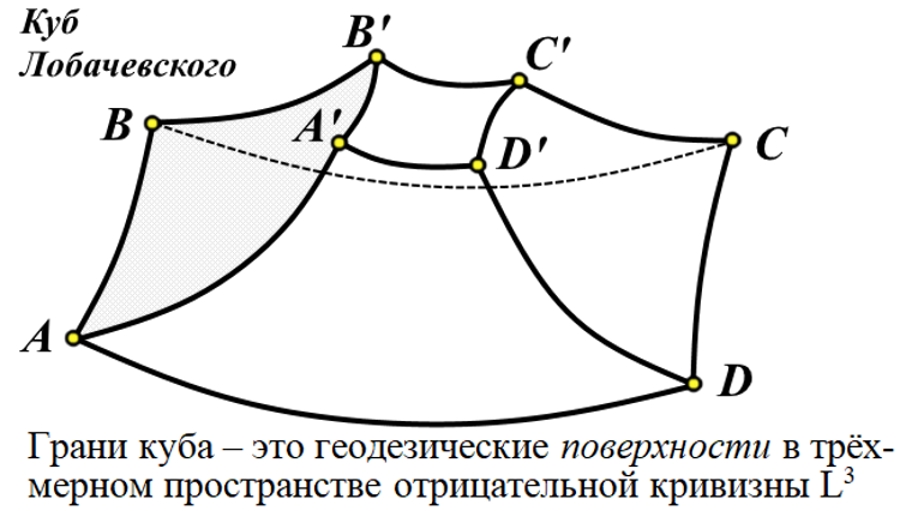
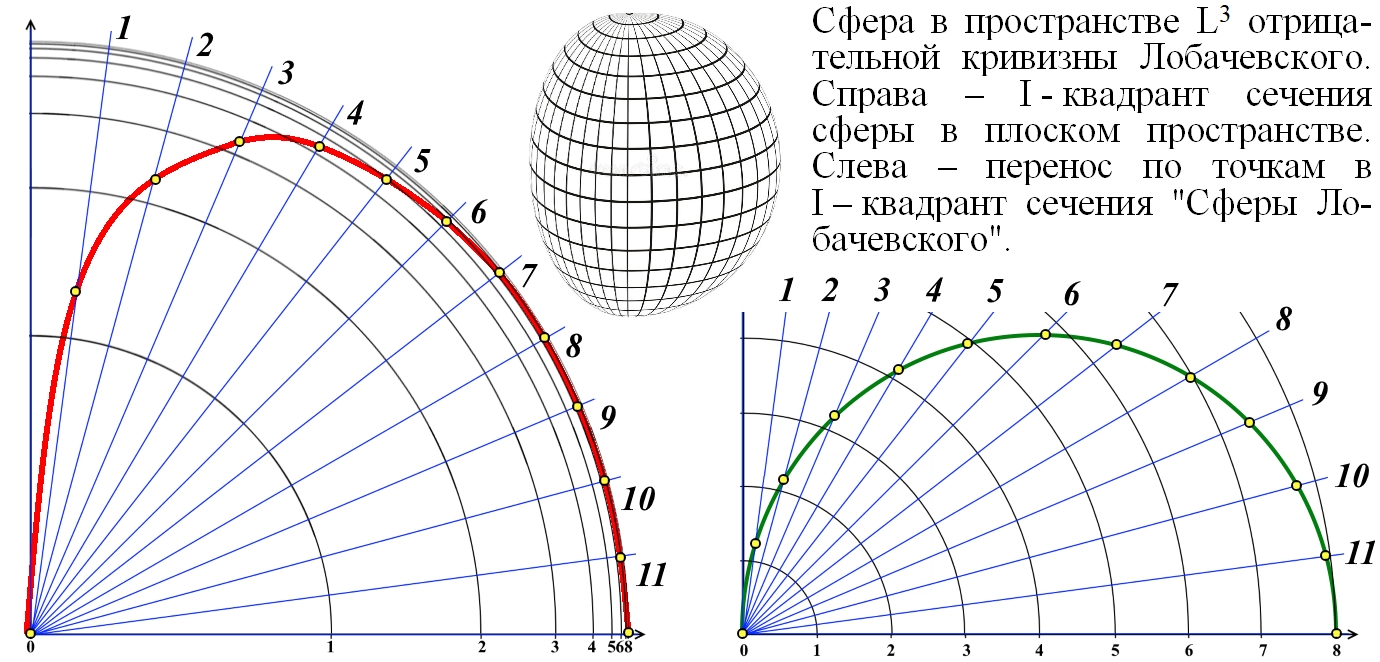
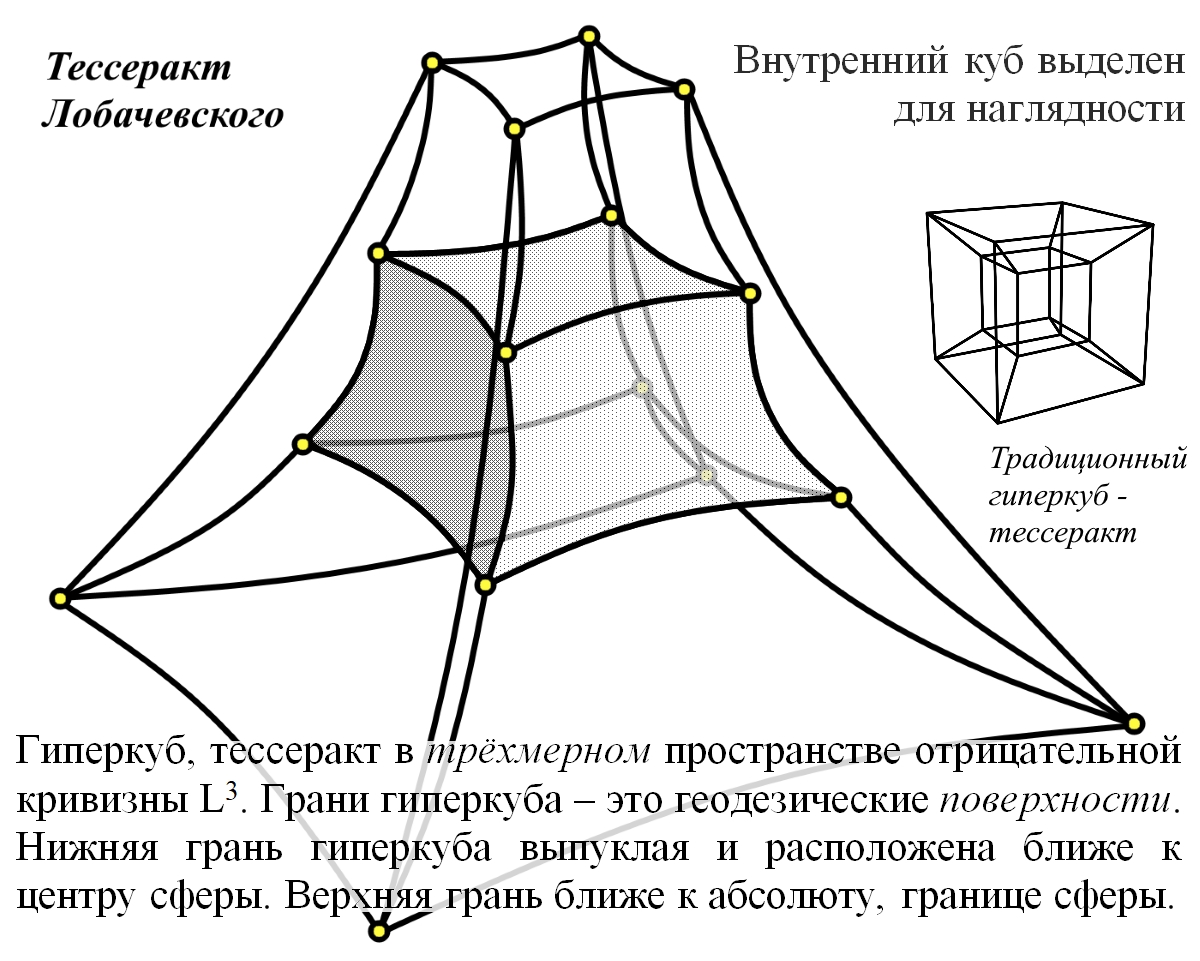
    Рассмотрено бесконечное трёхмерное пространство отрицательной кривизны Лобачевского. Бесконечное пространство радиально деформировано, сжато до шара конечных размеров. Конструкция является симуляцией, то есть реально такое пространство невозможно. Шару присвоено название "Сфера Лобачевского". Для радиального сжатия может быть использована тангенциальная, степенная и другие конечные шкалы. Показано, что через любые три точки внутри шара может быть проведена лишь одна сфера, ортогональная к поверхности, абсолюту шара. Такая сфера является геодезической поверхностью внутри шара и через единственную точку может быть проведено любое число таких поверхностей. Пересечение не менее чем четырёх геодезических поверхностей создаёт тела, аналогичные телам в трёхмерном пространстве Евклида. В качестве иллюстраций приведены: скелетная схема гиперболического куба, куба в трёхмерном пространстве отрицательной кривизны; скелетные схемы тетраэдра, обычной сферы и гиперболического гиперкуба - тессеракта.
    An infinite three-dimensional space of negative curvature of Lobachevsky is considered. Infinite space is radially deformed, compressed to a ball of finite dimensions. The construct is a simulation, that is, in reality, such a space is impossible. The glob was named "Lobachevsky's Sphere". For radial compression, tangential, power and other finite scales can be used. It is shown that can be drawn through any three points inside the ball only one sphere , which is orthogonal to the surface of the ball, to the absolute of the ball. Such a sphere is a geodesic surface inside the sphere, and any number of such surfaces can be drawn through a single point. The intersection of at least four geodesic surfaces creates bodies similar to bodies in three-dimensional Euclidean space. As illustrations are given: skeletal diagram of a hyperbolic cube, that is, a cube in three-dimensional space of negative curvature; skeletal diagrams of a tetrahedron, an ordinary sphere and a hyperbolic hypercube - a tesseract.

    •    Оглавление
       Диск Пуанкаре
       Сфера Лобачевского
       Трёхмерные тела отрицательной кривизны
       Гиперкуб гиперболический
       Заключение
       Литература
      
       Диск Пуанкаре
      
       В одной из прошлых работ [6] мы рассмотрели вопрос построения геодезических на поверхности отрицательной кривизны, гиперболической поверхности Лобачевского. Поверхность была представлена симуляцией на диске Пуанкаре. Целью этого исследования было разработать методику построения геодезических по двум заданным на диске точкам. Методика была разработана, и строго математически доказана её корректность.
       Использование методики позволило создать иллюстрацию эквиуглового перемещения вектора по замкнутому контуру на поверхности Лобачевского, на поверхности отрицательной кривизны. Как и для сферической поверхности было показано, что при таком перемещении вектор возвращается в исходную точку с поворотом, то есть, его направление не совпадает с исходным. Эквиугловое перемещение означает такое перемещение, при котором угол между вектором и геодезической траекторией переноса остаётся неизменным. Отмечено также, что параллельное перемещение векторов в искривлённом пространстве не имеет смысла.
       Перемещение на двухмерной поверхности отрицательной кривизны, на диске Пуанкаре является частным случаем. Математический механизм, заложенный в дисковую симуляцию двухмерной поверхности Лобачевского, допускает расширение модели на трёхмерное пространство отрицательной кривизны L3. Наряду с двухмерным диском Пуанкаре возможна трёхмерная модель, которую мы назвали сферой Лобачевского. Правильнее, конечно, называть её шаром, но "шар Лобачевского", на наш взгляд, название менее благозвучное. Нам неизвестны упоминания в литературе описываемой модели, поэтому мы и решили сами присвоить ей название. Как и двухмерный диск Пуанкаре, сфера Лобачевского является такой же симуляцией, но трёхмерной, также не имеющей реального воплощения [6].
       Пространство Лобачевского может быть представлено в виде разнообразных геометрических тел: псевдосфера Бельтрами, катеноид, поверхность Куена и другие [3]. Основой всех этих тел, их поверхностей являются некие абстрактные поверхности постоянной отрицательной кривизны:
       "Геометрия плоскости Лобачевского реализуется на поверхностях постоянной отрицательной кривизны в следующем смысле. Односвязный кусок такой поверхности всегда можно взаимно однозначно отобразить на кусок плоскости Лобачевского с сохранением длин всех кривых, углов между ними, площадей всех фигур и т.д. Геодезические линии поверхности отображаются при этом в прямые плоскости Лобачевского" [4, с.407].
       Звучит это несколько странно, поскольку поверхность, пространство Лобачевского такой поверхностью является по определению. Реальной, физической поверхности Лобачевского постоянной отрицательной кривизны не существует. Не существует полной и регулярной поверхности, внутренняя геометрия которой представляла бы геометрию полного пространства Лобачевского, поверхности постоянной отрицательной кривизны:
       "... не удаётся с помощью ни одной из известных до сих пор поверхностей постоянной отрицательной кривизны осуществить целиком всю плоскость Лобачевского" [1, с.304]
       "... не существует аналитической поверхности постоянной отрицательной кривизны, не имеющей нигде особенностей и повсюду регулярной ... на ... вопрос о том, можно ли ... осуществить в евклидовом пространстве на некоторой регулярной аналитической поверхности всю плоскость Лобачевского, надо ответить отрицательно" [1, с.311].
       Поскольку диск Пуанкаре имеет неравномерно сжатый, деформированный радиальный масштаб, на нём геодезические имеют вид окружностей лишь условно. Геодезические в виде окружностей -кажущаяся форма. Это хорошо заметно, если рассмотреть шкалу расстояний на диске. От центра к периферии радиальные отрезки сокращаются вплоть до нуля. Если вернуть шкалу расстояний в обычный, равномерный ряд, то все окружности окажутся непропорционально вытянутыми, примут форму гипербол
       На следующем рисунке представлены два геодезических треугольника, то есть, треугольники, ограниченные геодезическими, ортогональными окружностями на диске Пуанкаре, на котором они считаются прямыми линиями на поверхности отрицательной кривизны.

    Сфера Лобачевского

       Рис.1. Построение геодезических треугольников из ортогональных окружностей на диске Пуанкаре (слева) и из производных для них гипербол в плоском пространстве (справа)
      
       Слева приведено традиционное изображение таких треугольников ABC и CDE. Диск Пуанкаре является бесконечной плоскостью, сжатой в диск конечных размеров, вследствие чего его шкала расстояний и стала неравномерной. Справа этот диск возвращён в состояние с равномерной, обычной шкалой, но теперь уже отражающий лишь небольшой участок бесконечной плоскости. Поскольку на обоих дисках использована полярная система координат, углы радиус-векторов изображены одинаковыми. По соответствующим, одинаковым радиус-векторам и по шкалам, по точкам, вручную справа геодезические изображены такими, какими они видны в реальности. Очевидно, линии имеют форму гипербол. Поверхность отрицательной кривизны, следовательно, можно называть гиперболической поверхностью, двухмерным пространством. Отметим, что такое сжатие равномерной шкалы до размеров сферы не является конформным. На рисунке видно, что углы различаются. Особенно это заметно на углах CDE: слева он почти прямой, а справа заметно приближается к двум прямым.
      
       Сфера Лобачевского
      
       Рассматривая сферу Лобачевского, мы, как и в случае с диском Пуанкаре, ставим очевидную задачу проведения геодезической линии через две произвольные точки в трёхмерном пространстве Лобачевского. На следующем рисунке это точки B и P. Учитывая, что пространство трёхмерное, мы вводим понятие геодезической поверхности Лобачевского. Это означает, что в таком пространстве мы можем построить не только условно плоский криволинейный треугольник или любую фигуру с другим числом вершин. Теперь мы можем построить в ней тело с не менее чем четырьмя вершинами, например, гиперболический тетраэдр, ограниченный четырьмя геодезическими треугольниками. Такое тело - единственное, поскольку через любые три точки L3 пространства мы можем провести только одну геодезическую поверхность - сферу. Правда, в этом случае возникает неявное ограничение. Формально для ортогональной сферы ещё одна точка уже как бы задана - точка ортогональности сфер. Поэтому третья вершина треугольника - это четвёртая точка, и она также должна лежать на уже сформированной ортогональной сфере. Геодезические поверхности имеют определяющее свойство: это сферы, которые пересекают сферу Лобачевского ортогонально, что совпадает со свойствами геодезических на диске Пуанкаре. Легко показать, что сфера, ортогональная к данной сфере, ортогональна в любой точке пересечения этих сфер. Достаточно рассмотреть систему таких двух сфер относительно оси, проходящей через их центры. Вследствие симметрии, все точки линии пересечения равноценны. Если в одной из них сферы ортогональны друг другу, то автоматически они ортогональны во всех других.
       Также отметим, что любая плоскость, проходящая через центры сфер, вырезает, создаёт обычную систему с диском Пуанкаре и ортогональными окружностями - геодезическими линиями. Напомним, что и у диска Пуанкаре и у сферы Лобачевского радиус нелинейный. По мере удаления от центра, единичные отрезки на радиусах уменьшаются, вследствие чего эквивалентная длина радиуса стремится к бесконечности. Мы используем степенной закон деформации: интервалы вдоль радиуса сокращаются по обратным степеням двойки. Принципиально это не отличается от тангенциальной деформации осей на диаграммах Пенроуза.
       Вследствие симметрии, ортогональных сфер любого радиуса к заданной точке внутри сферы Лобачевского может быть бесконечное множество. Точнее, на порядок больше, чем ортогональных окружностей на диске Пуанкаре, условно говоря, в ∞2 раз больше. Линия центров диска Пуанкаре при этом превращается в плоскость центров ортогональных сфер.
       Для построения искомой геодезической проведём секущую плоскость через центр A сферы Лобачевского и две выбранные точки B и P. В пространстве погружения Евклида E3 через три точки можно провести только одну плоскость. Следовательно, используя математику инверсных точек, мы можем построить только одну, единственную геодезическую окружность, с которой, соответственно, будет связана единственная ортогональная сфера с центром в этой плоскости.
       Методика построения ортогональной окружности, геодезической полностью совпадает с описанной в [6]. Приведём частично описание и рисунок из этой работы, адаптируя их к сфере. Для наглядности на сфере мы используем те же самые обозначения, что и в указанной работе.

    Сфера Лобачевского

    Рис.2. Рисунок из статьи [6, рис.5]. Построение окружности, ортогональной к границе диска Пуанкаре

      
       Проведём на секущей плоскости линию через центр сферы, то есть, через центр образовавшейся окружности, и первую точку B искомой геодезической. Восстановим в точке B перпендикуляр до пересечения с окружностью в точке D и затем проведём к окружности в этой точке касательную до пересечения с линией AB. Точку пересечения обозначим буквой C. Легко показать, что образовавшиеся треугольники отвечают соотношению AB × AC = R2 для точек B и C, получивших название инверсных. Перпендикуляр к середине этого отрезка BC является линией центров ортогональных окружностей к образовавшейся окружности, эквиваленту диска Пуанкаре с центром в A и радиусом R сферы Лобачевского. Иначе говоря, центр любой ортогональной окружности, построенной по описанной методике и проходящей через точки B и C, естественно, находится на перпендикуляре к центру этого отрезка. Доказательство этого приведено в [6].

    Сфера Лобачевского

       Рис.3. Сфера (шар) Лобачевского. Левая сфера - симуляция трёхмерного пространства отрицательной кривизны Лобачевского L3. Правая сфера - ортогональная окружность, геодезическая, проходит через две заданные точки B и P
      
       Поскольку окружность может быть любого радиуса, то легко найти такую, которая будет проходить и через вторую заданную точку P. Для нахождения её центра нужно провести перпендикуляр через середину отрезка BP до пересечения с линией центров. Ясно, что методика позволяет построить только одну, единственную такую окружность.
       Для заданных двух точек мы провели единственно возможную секущую плоскость. На этой плоскости мы построили единственно возможный центр ортогональной окружности. Построив вокруг этой окружности сферу, мы получим единственно возможную сферу с центром в этой плоскости, ортогональную к выбранной сфере Лобачевского.
       Для дальнейших выкладок мы воспользуемся описанием одной замечательной точки треугольника - точки пересечения перпендикуляров к центрам его сторон:
       "Серединный перпендикуляр ... - прямая, перпендикулярная данному отрезку и проходящая через его середину. ... Серединные перпендикуляры к сторонам треугольника ... пересекаются в одной точке - центре описанной окружности" [5].
       Присвоим этой точке пересечения серединных перпендикуляров собственное имя - срединная точка. В дополнение к описанию этой замечательной точки треугольников в планиметрии добавим её расширенный вариант в стереометрии:
       Перпендикуляр, восстановленный к срединной точке треугольника, является осью фигур вращения, проходящих через вершины треугольника. В частности, на этой оси расположены центры бесконечного количества сфер, диаметром, не менее диаметра описанной окружности.
       Для рассматриваемого нами трёхмерного пространства отрицательной кривизны, сферы Лобачевского сформулируем также и своеобразный аналог 5-го постулата Евклида как дополнение к его вариантам для двухмерных пространств положительной и отрицательной кривизны:
       Через точку, лежащую вне заданной геодезической поверхности можно провести бесконечное число "параллельных" геодезических поверхностей, то есть, поверхностей, не пересекающих заданную.
       Слово "параллельных" мы взяли в кавычки, поскольку понятия параллельных криволинейных поверхностей не определено, как не определено корректно и понятие параллельных линий в искривлённых пространствах. В отличие от диска Пуанкаре, в сфере Лобачевского понятие равнобежных (асимптотически параллельных) поверхностей в данном случае имеет весьма условный смысл ввиду их бесконечного числа. В варианте, когда внешняя точка расположена над центром заданной геодезической поверхности, сохраняется понятие особой ультрапараллельности - это единственная геодезическая поверхность, симметрично расположенная по отношению к заданной поверхности: точка и центры сферы и двух геодезических находятся на одной линии.
       Следующий рисунок поясняет формирование алгоритма построения геодезической поверхности, заданной тремя точками внутри сферы Лобачевского. Главное условие - геодезическая поверхность, сфера должна быть ортогональна к сфере Лобачевского. Как известно, через произвольные три точки можно провести любое число сфер, сфер разного диаметра. Это прямо следует из свойств замечательной точки треугольника - точки пересечения перпендикуляров к центрам его сторон. Эта срединная точка является центром описанной вокруг треугольника окружности. Но, очевидно, что любая окружность может быть окружностью, сечением сферы любого диаметра, не меньшего диаметра окружности. Следовательно, и стороны заданного треугольника BEG также могут быть хордами любой такой сферы.

    Сфера Лобачевского

       Рис.4. Левая сфера - сфера (шар) Лобачевского, симуляция трёхмерного пространства отрицательной кривизны Лобачевского L3. Правая сфера - геодезическая поверхность в сфере Лобачевского. Проходит через углы треугольника BEG внутри сферы и инверсные точки B и C, которые отвечают уравнению AB × AC = R2. Точка K - пересечение медиатрис, серединных перпендикуляров к сторонам треугольника BEG. На перпендикуляре KH находятся центры всех геодезических сфер, проходящих через вершины треугольника. Плоскость (серая) - образуется вращением оси центров ортогональных окружностей вокруг оси BC.
      
       Рассмотрим треугольник BEG и его срединную точку K. Восстановим в ней перпендикуляр бесконечной длины. Выберем на перпендикуляре произвольную точку H и соединим её с вершинами треугольника. Рассмотрим далее прямоугольную пирамиду с вершиной H и основанием EKG. Две её грани равны: EKH и GKH, поскольку обе они - прямоугольные треугольники, имеющие по две равные стороны: EK = GK, как радиусы описанной окружности, и общая - KH. Из этого следует, что и третьи их стороны равны: EH = GH. Рассмотрев аналогично две другие грани, приходим к выводу, что все рёбра пирамиды равны: EH = GH = BH. Поскольку мы имеем три точки B, E и G, одинаково удалённые от третьей точки H, мы можем провести через них сферу радиусом, равным длине этих рёбер.
       Поскольку точку H мы выбрали произвольно, значит через эти три точки B, E и G мы можем провести сферу любого радиуса. Все центры сфер при этом лежат на перпендикуляре к срединной точке треугольника. Поэтому мы дадим ему с некоторым опережением название - линия центров геодезических. С опережением, поскольку мы пока не уверены, что эта сфера будет ортогональна к нашей сфере Лобачевского.
       Для дальнейших рассуждений повторим сделанные ранее построения, подобные построениям на диске Пуанкаре. Проведём из центра A сферы Лобачевского через одну из вершин выбранного треугольника B произвольную плоскость, и через неё же - линию. В плоскости проведём перпендикуляр к точке B до пересечения со сферой в точке D. Проведём к этой точке радиус DA и касательную к сфере, ортогональную к этому радиусу. Точку пересечения касательной и линии, проходящей через точки AB, обозначим буквой C. Как известно, эти две точки - B и C называются инверсными и отвечают соотношению AB × AC = R2. Проведём через середину F отрезка BC в созданной плоскости перпендикуляр. По построению плоскость является полным аналогом диска Пуанкаре, поэтому прямая из F является линией центров окружностей, ортогональных к границе полученного диска Пуанкаре, то есть, геодезических на диске.
       Приведём во вращение плоскость и диск вокруг линии AC. Очевидно, точка D опишет на сфере Лобачевского окружность, а радиус DA и касательная DC очертят два конуса. Соответственно, перпендикуляр в точке F - очертит бесконечную плоскость, ортогональную к линии AC, которую обозначим для краткости и определённости как плоскость F.
       Рассмотрим сущность этой плоскости. Каждая линия на ней, проходящая через точку F для каждого положения вращаемой плоскости, всегда, обязательно входит в какую-то группу с треугольником ADC, которая в каждом из этих случаев описывается соотношением AB × AC = R2, то есть, линия через F является линией центров ортогональных окружностей, проходящих через точки B и C.
       Поскольку линия центров геодезических из точки K не параллельна плоскости F, она её пересечёт в некоторой неизвестной точке H. В случае параллельности линии из K и плоскости F примем, что точка H находится в бесконечности.
       Поскольку эта точка H находится на линии центров сфер из точки F, проходящих через вершины треугольника BEG, и одновременно на плоскости F, являющейся плоскостью центров геодезических сфер, эта точка H автоматически становится центром сферы, проходящей через заданные точки, вершины треугольника BEG и инверсную точку C. Таким образом, эта сфера автоматически оказывается ортогональной к абсолюту, границе сферы Лобачевского. Что нам и требовалось найти.
       Однако, пока нам неясно, как определить точное положение этой точки H. Очевидны два варианта построений: геометрические и аналитически. Во втором случае нам необходимо все параметры системы представить в аналитическом, числовом виде. Координаты центра сферы Лобачевского, очевидно, мы зададим нулевыми. Координаты вершин треугольника - обычными координатами либо в полярной системе координат, либо в некой условной декартовой; условной ввиду неравномерности интервалов. На рис.3 и рис.5 мы изобразили эту неравномерность на отдельном радиусе сферы.
       В общих чертах смысл метода определён, но для дальнейших однозначных построений нам необходимо ввести третью координатную ось z или второй полярный угол. Следующий рисунок является копией предыдущего рис.4 с добавленной третьей декартовой координатой. С рисунка мы удалили теперь уже лишние линии, затеняющие его.

    Сфера Лобачевского

       Рис.5. Усечённая версия рис.4. Слева - сфера Лобачевского, симуляция трёхмерного пространства отрицательной кривизны. Сфера справа - геодезическая поверхность в сфере Лобачевского.
      
       Для окончательных геометрических построений с целью геометрического определения точного положения точки H нам необходимы все три проекции объектов на рисунке. Для удобства, необходимо объекты на рисунке сначала развернуть таким образом, чтобы плоскость xAy совпала с плоскостью рисунка. Затем добавить проекции плоскостей zAy и zAx, на которых следует показать положения вершин треугольника BEG. В результате построений точка H получит единственно возможное положение.
       Для соответствующих аналитических построений нам необходимы пространственные, численные координаты всех точек: в декартовой или сферической системах координат. Координаты точки H мы получим также в численном виде.
       Заметим, что оба варианта достаточно трудоёмки и, вместе с тем, уже не дадут какой-либо ещё принципиально необходимой информации. Приведённого доказательства единственности точки H нам уже достаточно, поэтому дальнейшие построения и вычисления мы прекращаем.
      
       Трёхмерные тела отрицательной кривизны
      
       Наличие у пространства трёх координат прямо предполагает возможность создания в нём объектов, имеющих какой-то объём. Основным, главным классом таких объектов, тел следует признать объекты, образованные геодезическими поверхностями, причём объекты должны быть замкнутыми. Геодезическая поверхность в соответствующем искривлённом пространстве - это эквивалент плоскости Евклида. В рассмотренном пространстве отрицательной кривизны Лобачевского, в сфере Лобачевского такими поверхностями являются ортогональные сферы. Тело, образованное не более чем тремя геодезическими поверхностями в сфере Лобачевского, будет незамкнутым, с одной стороны оно будет открыто до бесконечности. В геометрии Евклида сказано:
       "... две прямые не содержат пространства" [2, с.15].
       В стереометрии и в рассматриваемом трёхмерном пространстве Лобачевского справедливо подобное утверждение: три плоскости или три геодезические двухмерные поверхности пространства не содержат. В сфере Лобачевского замкнутый объект, как и в пространстве Евклида, могут образовать, как минимум, четыре геодезических поверхности.
       Замкнутость означает невозможность попасть внутрь объекта извне, не пересекая его границы. Иначе говоря, такие тела имеют двухстороннюю границу. Как и в пространстве Евклида, объектом с наименьшим числом граней в сфере Лобачевского является четырёхгранник, в частности, тетраэдр. Для его построения необходимо построить четыре геодезические поверхности, проходящие через четыре точки, не лежащие в одной геодезической плоскости, поверхности. Далее для простоты изображение тетраэдра в трёхмерном пространстве отрицательной кривизны мы приведём схематично.

    Сфера Лобачевского

       Рис.6. Грани тетраэдра - это геодезические поверхности в трёхмерном пространстве отрицательной кривизны L3
      
       Верхняя вершина тетраэдра D находится к абсолюту сферы Лобачевского ближе остальных. Все грани, кроме нижней, вогнуты. Нижняя грань - выпуклая, она образована самой большой геодезической поверхностью, и весь тетраэдр находится внутри неё. Для построения тетраэдра мы не стали производить достаточно сложные стереометрические построения, нагружать иллюстрацию многочисленными "строительными лесами".
       Следующим по сложности объектом, очевидно, должен быть пятигранник. Однако это достаточно редкий объект, поэтому сразу переходим к самому распространённому - кубу. Механизм его построения тот же - необходимо через восемь точек провести шесть геодезических поверхностей, ортогональных сфер, граней куба. Выбор точек проще сделать аналитически - задать их координаты таким образом, чтобы каждая точка находилась на одном и том же расстоянии от трёх ближайших. Как и в случае тетраэдра, здесь мы также не делаем сложных стереометрических построений, а приводим схематичную иллюстрацию. Она довольно далека от точных построений, но достаточно точно отображает вид объекта - куба в трёхмерном пространстве отрицательной кривизны.

    Сфера Лобачевского

       Рис.7. Грани куба - это геодезические поверхности в трёхмерном пространстве отрицательной кривизны L3. Нижняя грань куба - выпуклая и расположена ближе к центру сферы Лобачевского.
      
       На рисунке верхняя, меньшая грань куба A'B'C'D' находится ближе к абсолюту, границе сферы Лобачевского. Все грани, кроме нижней, вогнуты. Нижняя грань ABCD образована самой большой геодезической поверхностью и весь куб находится внутри неё.
       Следующим широко распространённым объектом, имеющим объём, является сфера. Понятно, что ни в пространстве Евклида, ни, видимо, в любом другом трёхмерном пространстве сфера не может быть образована "внутренними плоскостями", геодезическими поверхностями. Главная причина в том, что сфера и другие объекты, ограниченные криволинейными поверхностями, внутренними для пространства, по сути, являются объектами, погружёнными в это пространство. Иначе говоря, чужеродными объектами. Проявляется это, в частности, в том, что на этих чужеродных объектах присутствуют принципиально иные геодезические.
       Например, в рассмотренную нами сферу Лобачевского, трёхмерное пространство, мы можем без деформаций поместить обычную евклидову сферу. Из пространства погружения мы и будем видеть её именно как идеально симметричный объект, сферу, на которой есть собственные геодезические - большие круги. У этой сферы - собственный параллельный перенос вектора по замкнутой траектории с опережающим поворотом при возврате. Наконец, у неё есть собственный треугольник с суммой углов, превышающих два прямых. Однако, с точки зрения наблюдателя в сфере Лобачевского, сфера эта будет выглядеть как довольно экзотический объект. Рассмотрим теперь другой процесс - эквивалентный перенос в сферу Лобачевского обычной сферы из пространства погружения. Для этого рассмотрим первый квадрант сечений сферы Лобачевского, слева, и её же, но без радиальной деформации, справа. Для простоты построения шкалы, длин радиус-векторов, мы используем её деление по степеням двойки: длина первого отрезка равна 2-0, второго - 2-1, третьего - 2-2 и так далее. При таком делении, уже отметка 8 в сфере Лобачевского практически сливается с границей сферы, с абсолютом. Поэтому будем использовать только 8 точек на радиус-векторах.

    Сфера Лобачевского

       Рис.8. Сфера в пространстве L3 отрицательной кривизны Лобачевского. Справа: I-ый квадрант сечения сферы в плоском пространстве. Слева: перенос по точкам сечения в I-ый квадрант "Сферы Лобачевского".
      
       Окончательные сферы получим вращением этих сечений вокруг горизонтальной оси. Полярные углы в обоих сечениях тождественны, мы рассматриваем только 13 положений - от 0 до 12. В каждом из этих положений определяем длину радиус вектора в плоском, недеформированном пространстве. Затем откладываем это расстояние в сечении сферы Лобачевского, учитывая, разумеется, её шкалу расстояний. После нанесения всех 13 точек, соединяем их плавной кривой и производим вращение вокруг горизонтальной оси. Как и выше, здесь мы также не проводим замысловатых стереометрических построений полученной сферы, а сразу же приводим её схематичное изображение - средняя часть рисунка.
       Очевидно, при обратном переносе по точкам описанной выше евклидовой сферы из сферы Лобачевского в пространство погружения мы будем видеть её неравномерно вытянутой, деформированной.
      
       Гиперкуб гиперболический
      
       Мы показали возможную реализацию трёхмерного пространства отрицательной кривизны, пространства Лобачевского, и показали несколько объёмных тел в этом пространстве. Возникает естественное предположение о возможности дальнейшего расширения этого пространства, увеличения числа его измерений. В трёхмерном пространстве Евклида изобразить объекты четырёхмерного пространства практически невозможно. Например, имеющиеся изображения четырёхмерного куба, тессеракта выглядят весьма отвлечённо. Тем не менее, его изображение в литературе и в фильмах встречается довольно часто. Исходя из этого, мы делаем естественное предположение, что такой же тессеракт можно изобразить и в сфере Лобачевского. Скелетный вариант такого гиперболического гиперкуба можно изобразить в следующем виде:

    Сфера Лобачевского

       Рис.9. Гиперкуб, тессеракт в трёхмерном пространстве отрицательной кривизны L3. Грани гиперкуба - это геодезические поверхности. Нижняя грань гиперкуба выпуклая и расположена ближе к центру сферы. Верхняя грань ближе к абсолюту, границе сферы. Внутренний куб выделен для наглядности
      
       Заключение
      
       Сфера Лобачевского является симуляцией трёхмерного пространства отрицательной кривизны L3. Формально она содержит в себе всё бесконечное пространство, всю соответствующую ему Вселенную. Однако рассмотренная сфера - это деформированное, искажённое пространство, которое реально существовать не может, также как, согласно "мягкому" замечанию Гильберта, не удаётся осуществить целиком и плоскость отрицательной кривизны.
       В пространстве сферы Лобачевского можно осуществить традиционный эквиугловой перенос вектора по замкнутому контуру. В этом случае вектор уже не нужно рассматривать как элемент касательного пространства, теперь он имеет вполне определённое собственное пространственное направление. При возвращении вектора в исходное положение его направление в общем случае будет иным. Например, если произвести перенос по контуру грани тетраэдра или куба, то вектор, всегда ортогональный к грани, при возврате в исходную точку совпадёт с исходным, поскольку все векторы, ортогональные грани, направлены в сторону центра соответствующей геодезической поверхности, сферы.

    04.11 - 14.11.2021

       Литература
      
       1. Гильберт Д. "Основания геометрии", пер. с 7-го немецкого издания И.С.Градштейна, Москва - Ленинград, ОГИЗ, Гос. изд. тех.-теор. лит-ры, 1948 г.
       2. Евклид, "Начала", книги I-VI, пер. с греч. и комментарии Д.Д.Мордухай-Болтовского, ОГИЗ, Гос. изд. тех.-теор. лит-ры, Москва - Ленинград, 1950 г.
       3. Попов А.Г. Псевдосферические поверхности и некоторые задачи математической физики, МГУ им. М. В. Ломоносова, Фундаментальная и прикладная математика, 2005, том 11, N 1, с. 227 - 239. (с)  2005, Центр новых информационных технологий МГУ, Издательский дом "Открытые системы"
       4. Рашевский П.К. Курс дифференциальной геометрии. - М.-Л., ГИТТЛ, 1950
       5. Серединный перпендикуляр, Википедия, URL: https://ru.wikipedia.org/wiki/Серединный_перпендикуляр
       6. Путенихин П.В. Перенос вектора на поверхности отрицательной кривизны. Диск Пуанкаре, Самиздат, URL:
            http://samlib.ru/editors/p/putenihin_p_w/diskpuank.shtml
            http://lit.lib.ru/editors/p/putenihin_p_w/diskpuank.shtml
       7. Путенихин П.В. Трёхмерное пространство отрицательной кривизны. Сфера Лобачевского, Самиздат, URL: http://samlib.ru/editors/p/putenihin_p_w/sphelobach.shtml
      
  • Оставить комментарий
  • © Copyright Путенихин Петр Васильевич (pe_put@rambler.ru)
  • Обновлено: 14/11/2021. 36k. Статистика.
  • Статья: Естеств.науки
    •  Ваша оценка:
    Связаться с программистом сайта.